Mathematics can be intimidating when problems stretch beyond the basics, especially when it comes to integrals that don’t immediately look “friendly.” Yet, there’s a rhythm to solving even the most intimidating integrals.
Once you break them down step by step, the fog lifts, and what seemed impossible becomes manageable. That’s exactly what we’re going to do here: walk through methods, real examples, and practical techniques that can help anyone sharpen their integral-solving skills.
Instead of treating integrals as abstract monsters, we’ll approach them as puzzles with patterns to spot and strategies to unlock. You’ll see not only how to work through them, but also why certain tricks matter, so you can apply them to new problems with confidence.
What Makes an Integral “Complex”?
Not every integral falls into the simple “apply the power rule” category. A complex integral might involve:
- Functions without obvious antiderivatives (like trigonometric or exponential combinations)
- Rational functions that require algebraic manipulation
- Improper integrals stretching to infinity or involving singularities
- Integrals that need special techniques, such as substitution, integration by parts, or partial fractions. The key is not to panic when you see a tough one – it’s the same calm approach you’d use when tackling combinatorics problems.
The key is not to panic when you see a tough one. Think of it as sorting through a toolbox: each technique is a tool, and your job is to pick the right one.
Core Strategies to Keep in Mind

1. Direct Antiderivatives
Apply standard formulas (like ∫xⁿ dx = (xⁿ⁺¹)/(n+1) + C, for n ≠ -1).
2. Substitution (u-substitution)
Useful when you spot a function and its derivative inside the integral.
3. Integration by Parts
Best for products of functions, based on the formula:
∫u dv = uv – ∫v du
4. Partial Fractions
Break down rational functions into simpler fractions that are easier to integrate.
5. Trigonometric Identities
Transform trigonometric integrals using identities (like sin²x + cos²x = 1).
6. Improper Integral Handling
Use limits to evaluate infinite ranges or undefined points.
Step-by-Step Examples

1. Substitution Example
Let’s start with something manageable:
∫ 2x cos(x²) dx
Step 1: Spot the inner function
x² is inside the cosine, and its derivative (2x) is sitting outside. That’s the sign for substitution.
Step 2: Set substitution
Let u = x². Then du = 2x dx.
Step 3: Rewrite the integral
∫ cos(u) du
Step 4: Integrate
∫ cos(u) du = sin(u) + C
Step 5: Back-substitute
Answer: sin(x²) + C
This is the cleanest type of substitution integral. Spotting the derivative alongside the inner function is the trick.
2. Integration by Parts Example
View this post on Instagram
Now, let’s take on: ∫ x e^x dx
Step 1: Choose u and dv
A good rule: pick u as the algebraic function (x) and dv as the exponential (e^x dx).
- u = x → du = dx
- dv = e^x dx → v = e^x
Step 2: Apply the formula
∫u dv = uv – ∫v du
So: ∫ x e^x dx = x e^x – ∫ e^x dx
Step 3: Simplify
= x e^x – e^x + C
That’s it. Integration by parts often shines when you see a product of polynomials and exponentials or trigonometric functions.
3. Partial Fractions Example
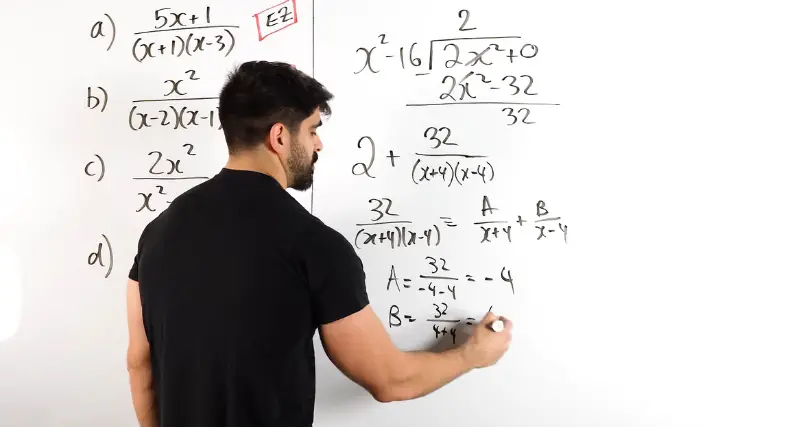
Now, for rational functions:
∫ (3x + 5) / (x² + 2x – 3) dx
Step 1: Factor the denominator
x² + 2x – 3 = (x + 3)(x – 1)
Step 2: Set up partial fractions
(3x + 5) / [(x + 3)(x – 1)] = A / (x + 3) + B / (x – 1)
Step 3: Multiply through by the denominator
3x + 5 = A(x – 1) + B(x + 3)
Step 4: Solve for A and B
Expand: 3x + 5 = (A + B)x + (-A + 3B)
Match coefficients:
- A + B = 3
- -A + 3B = 5
From first: A = 3 – B
Plug in: -(3 – B) + 3B = 5 → -3 + B + 3B = 5 → 4B – 3 = 5 → B = 2
Then A = 1
Step 5: Rewrite integral
∫ [1 / (x + 3) + 2 / (x – 1)] dx
Step 6: Integrate
= ln|x + 3| + 2 ln|x – 1| + C
This is the power of partial fractions, breaking something messy into bite-sized pieces.
4. Trigonometric Identity Example
@neildoesmaths Another Trignometric Proof For You🫡🔥 #trigonometry #trigonometricidentities #trigproofs #trigproof #alevelmaths #alevelmathshelp #neildoesmaths #myedspace ♬ original sound – NeilDoesMaths
Consider:
∫ sin²x dx
Step 1: Use identity
sin²x = (1 – cos2x) / 2
Step 2: Rewrite
∫ sin²x dx = ∫ (1/2)(1 – cos2x) dx
= (1/2) ∫ 1 dx – (1/2) ∫ cos2x dx
Step 3: Integrate
(1/2)x – (1/4) sin2x + C
So ∫ sin²x dx = (x/2) – (sin2x / 4) + C
When trig integrals show up, identities often cut down the difficulty dramatically.
5. Improper Integral Example

Evaluate:
∫₁^∞ (1 / x²) dx
Step 1: Write as a limit
∫₁^∞ (1 / x²) dx = lim(t→∞) ∫₁^t (1 / x²) dx
Step 2: Integrate
∫ (1 / x²) dx = -1 / x
Step 3: Apply bounds
= lim(t→∞) [-1/t + 1/1]
= 0 + 1 = 1
Even though it’s infinite in range, the integral converges to a finite value.
Common Pitfalls to Avoid
- Forgetting to back-substitute after using u-substitution
- Dropping constants of integration (+C) in indefinite integrals
- Ignoring domain restrictions when using logarithms in partial fractions
- Mixing up signs during integration by parts
Quick Reference Table of Techniques
| Type of Integral | Go-To Technique |
| Function with inside + derivative | Substitution |
| Product of polynomial and exponential | Integration by Parts |
| Rational function with factorable denom | Partial Fractions |
| Trigonometric powers | Identities or Substitution |
| Infinite bounds or discontinuities | Limits with Improper Integral |
Why Step by Step Matters

When problems grow messy, it’s tempting to skip small steps. But skipping leads to mistakes. Writing things out systematically helps catch errors, keeps your thoughts organized, and builds confidence.
Over time, you’ll find yourself spotting shortcuts naturally. Mathematics rewards patience, and integrals are no exception. If you can slow down, break them apart, and trust the process, even the ugliest problems fall into place.
Wrapping It Up
Solving integrals isn’t about memorizing hundreds of formulas-it’s about recognizing patterns and applying the right tools. From substitution and integration by parts to partial fractions and trigonometric tricks, each method has a clear purpose.
Many of Europe’s best education systems stress the same principle: teaching students to focus on problem-solving skills rather than rote memorization.
With practice, they stop feeling like random rules and start feeling like second nature. If you’re working through tougher problems, keep a sheet of core formulas nearby and don’t hesitate to work slowly.
Every expert who breezes through integrals once struggled with the same stumbling blocks. The only difference now is practice, structure, and knowing which tool to grab at the right time.

